Skip to main content

3.3.2 Costs

Costs 

Total cost - the total expense incurred in reaching a particular level of output. 

TC = TFC + TVC 

Total fixed cost - costs that do not vary with output. 
e.g rent, R&D, advertising

Total variable cost - costs that vary with output 
e.g raw materials, labour, power 

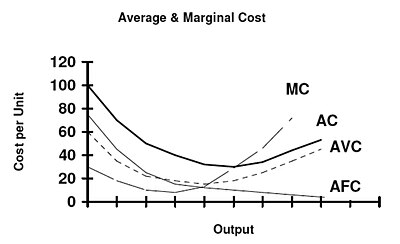
Average (total) cost - the cost in producing a unit output. Obtained through dividing TC by Q (quantity sold). 

ATC = TC/Q
Image result for cost curves

Average fixed cost - fixed cost in producing a unit output. AFC is not fixed - increasing the output spreads the TFC (a fixed quantity) and divides it, making it smaller and reducing the cost per unit output. 

NB: area under the AFC curve is TFC. 

AFC = TFC/Q 

Average variable cost - variable cost per unit output 

AVC = TVC/Q 

Marginal cost - equal to marginal variable cost as there are no marginal fixed costs. 
Image result for cost curves



 We define the short run as time in which at least one factor of production is fixed, and the long run as time in which all factors of production are variable. 

 i.e in the SR a firm can vary labour and not capital, in LR a firm is able to vary both. 

Law of diminishing returns/diminishing marginal productivity


 Diminishing returns occur where the marginal productivity falls. In the SR the presence of a fixed factor can put a constraint on the productivity of the variable factors. 

 As you add variable factors of production to a combination containing at least one fixed factor, the productivity of the variable factor will inevitably decline. (though at first it will rise) 

 e.g MIVs digging up potatoes(!) 
if there is only a fixed number of shovels, as you employ more MIVs the number of potatoes dug up will at first increase (as the shovels are put to use), and then still increase but at a decreasing rate as all the shovels are used and the extra MIVs are forced to dig with their hands/stand around and do nothing to increase output. 

This explains the parabolic shape of the AC curve - at first productivity increases, so the firms' cost per worker declines. After a certain point, however, the law of diminishing returns kicks in and the cost per worker rises, meaning the AC slopes upwards. 

 The TC curve reflects the law too - at first each additional unit doesn't add too much to the cost so the gradient is shallower, but as productivity decreases each additional unit adds more to the total cost and the curve slopes upwards at a steeper gradient. 

Relationship between SRAC and LRAC 

The LRAC shows the minimum possible cost of producing a given level of output with present technology. The firm is limited in the SR to varying output along the SRAC due to a fixed factor of production, and if it changes FoP it moves to a different SRAC. In the LR however, all FoPs are variable, so we get a LRAC that 'envelopes' all the SRAC. The LRAC touches each of the SRAC (not necessarily at their minima though). The SRACs cannot undercut the LRAC because SR costs are never lower than LR costs. 
Image result for LRAC

Labels:

Comments

Post a Comment

Popular posts from this blog

PPF

Production Possibility Frontier Production Possibility Frontier (PPF): the curve showing the maximum combinations of goods or services that can be produced in a given time with available resources. Assumptions: -         Production over a specific time period like one year -         Inputs are fixed during this time period -         Technology doesn’t change during this time period ·        Meaning of points on and around the PPF—efficiency When you are on the PPF, you are working at maximum efficiency or full capacity. If you are within the PPF then you are under-utilising existing resources or resources are being used inefficiently. There is underemployment. The economy cannot produce past the frontier. Points outside the PPF are unattainable given the current inputs. ·        Causes and me...
Post a Comment
Read more

3.1.3 Demergers

Demergers   A demerger is the breaking up of a firm into separate firms.  e.g Sports Direct selling off Dunlop in 2016. PepsiCo splitting off foods businesses (KFC, Taco Bell, etc.) into a separate corporation, Yum Brands. Later Yum Brands demerged into Yum China and Yum Brands. Reasons for demergers Diseconomies of scale - the opposite of economies of scale, where average costs begin to rise as output increases. May occur due to it being difficult to retain control on the expanding business - principal-agent problem may arise. Also less co-operation by employees who feel more alienated and as a result less productive - they feel less of a connection to the business.  May also be hard to co-ordinate and communicate between locations and employees when a firm is large. Miscommunication can again lead to costs rising.  To focus on core businesses to streamline costs and improve profits. The firm may have expanded into different markets and expe...
Post a Comment
Read more

The Philips curve

The Philips curve  The Philips curve suggests a tradeoff between unemployment and inflation - to decrease unemployment, inflation has to rise. This creates a conflict between two macroeconomic objectives - targeting inflation at 2% (in the UK) and decreasing unemployment. 
Post a Comment
Read more